Среднее арифметическое

Предлагаемая здесь программа расчета среднего арифметического умеет не только считать статистические параметры исследуемого множества чисел, но и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию...

Содержание:

• Определение среднего арифметического
• Расчет среднего арифметического
• Свойства среднего арифметического
• Прикладное значение среднего арифметического
• Задания ЕГЭ, на тему "Среднее арифметическое"

 

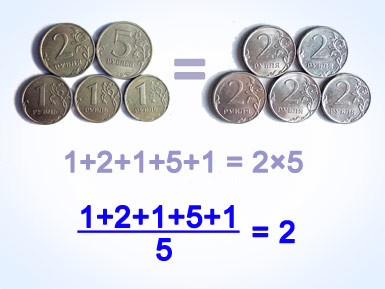Прежде чем начать что-либо считать будет уместно вспомнить определение предмета расчетов:

Среднее арифметическое^[1] значение (чаще используется термин, просто, "среднее арифметическое" или "среднее") множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

 

Для начала расчета введите исходные числа в одно из полей ввода-вывода данных.
В первое поле можно ввести последовательность чисел, разделенных точкой с запятой (программа попытается так же преобразовать к стандартному виду, например, вставленную копию последовательности чисел с плавающей точкой, разделенных пробелами, запятой или точкой с запятой).
Во второе поле можно вводить числа по одному - они автоматически будут добавляться к данным первого поля, если расчет не запустился автоматически, кликните по зеленой кнопке, показывающей количество чисел в исследуемом массиве:

 

Расчет среднего арифметического

 

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднего арифметического в истории браузера

Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднего арифметического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

Свойства среднего арифметического

1. Среднее арифметическое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.

2. Кроме того среднее арифметическое подчиняется неравенству о средних для множества положительных вещественных чисел

a_min   ≤   a_{ср. гарм}   ≤   a_{ср. геом}   ≤   a_{ср. арифм}   ≤   a _{ср.квадр} ≤   a _max ^[2*] ,

то есть для любого множества действительных чисел среднее арифметическое никогда не бывает больше среднего квадратического ^[1]:

 

Прикладное значение среднего арифметического

Среднее арифметическое значений исследуемых данных находит широкое прикладное применение в метрологии и статистике. При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение будет являться оценкой ошибки измерений, поэтому дисперсия и среднеквадратическое отклонение так же включены в результаты расчетов.

 

Задания ЕГЭ, на тему "Среднее арифметическое"

Задание 1:

Среднее арифметическое 7 натуральных чисел равно 12. К ним добавили восьмое число такое, что среднее арифметическое этих восьми чисел равно 14. Найдите восьмое число.

Решение:

Согласно оределению среднего арифметического для 7 чисел имеем:

А для 8 чисел получется, что

откуда

S₇ = 12 × 7 = 84;

  S₇ + a₈ = 14 × 8 = 112;

 a₈ = 112 - S₇ = 112 - 84 = 28;

Ответ: a₈ = 28

 

Задание 2:

На доске написано более 40, но менее 50 целых чисел. Среднее арифметическое этих чисел равно -4, среднее арифметическое всех положительных из них равно 5, а среднее арифметическое всех отрицательных из них равно -5.
а). Сколько чисел написано на доске?
б). Каких чисел написано больше: положительных или отрицательных?
в). Какое наибольшее количество положительных чисел может быть среди них?

Решение:

Пусть всего  n чисел, 40 < n < 50.
Пусть  k - количество положительных чисел, рассматриваемого множества;
m - количество отрицательных, и p - число нулей.
Тогда 

 k + m + p = n

по определению среднего арифметического сумма множества чисел равна призведению среднего арафметического и их количества и по условию задачи имеем: 

 5·k + -5·m + 0·p = -4·n   (2.1)

 5·(k - m) = -4·n      (2.2)

(включаем логику [обычную])

а). Очевидно, что левая часть полученного равенства 2.2 делится на 5, поэтому nтоже должно делиться на 5. По условию 40 < n < 50, отсюда

n = 45.

Таким образом, написано 45 целых чисел.

б). Подставим в равенство 2.2 полученное для n значение, тогда

 5·k + -5·m = -180   или   m - k = 36; m = 36 + k,   (2.3)

поскольку m ≥ 0 и k ≥ 0, то m > k, то есть отрицательных чисел больше, чем положительных.

в). Для определения наибольшего возможного количества целых положительных чисел удовлетворяющих условиям задачи, возпользуемся выражениями 2.1 и 2.3 с подставленным значением n. С учетом того, что p ≥ 0получаем:

k + m ≤ 45;
m = 36 + k

или подставляя в первое значение m:

2·k ≤ 45-36, k ≤ 4,5

Таким образом положительных чисел может быть не более 4.

Ответ: а) 45; б) отрицательных; в) 4.

 

P.S. На этой странице используется Бета версия программы расчета среднего арифметического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

 

1. Другие кому-то, возможно, более привычные определения:
Среднее арифметическое нескольких чисел равно сумме этих чисел,  делённой на количество слагаемых в этой сумме (Математика, 5 класс).
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых (Алгебра, Макарычев, 7 класс).

2. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:

 

3. Среднеквадратическое отклонение σ вычисляется как корень квадратный от дисперсий и возвращает нас в область сопоставимых со средним арифметическим величин:

.

4. Коэффициент вариации ряда чисел — мера относительного разброса их значений; показывает, какую долю от среднего значения этой величины составляет её средний разброс. Исчисляется в процентах:

 

5. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Таким образом, размах вариации может быть представлен следующей формулой:

R = a_max - a_min

6. Среднее линейное отклонение определяется как средняя арифметическая величина абсолютных значений отклонений каждого из ряда чисел от их среднего арифметического:

 

 

● Главная ▸ Статьи ▸ Блог ▸ Копилка ✔ Среднее арифметическое - онлайн расчет