Среднее геометрическое

Предлагаемая здесь программа, помимо расчета среднего геометрического, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию...

Содержание:

• Определение среднего геометрического
• Расчет среднего геометрического
• Свойства среднего геометрического
• Прикладное значение среднего геометрического

 

Среднее геометрическое или среднее пропорциональное используется человечеством в архитектурных, землемерных и инженерных расчетах не менее 2500 лет. Об этом достоверно известно благодаря математическому трактату Евклида "Начала".
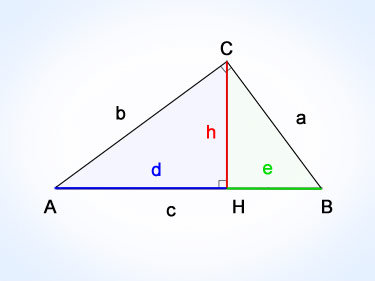
В своей второй теореме Евклид доказывает, что в прямоугольном треугольнике высота проведенная из прямого угла (рисунок) делит противоположную сторону так что:

Собственно говоря, благодаря второй теореме Евклида среднее геометрическое и получило свое название. В древнем мире математики ограничивалось только использованием корня квадратного (геометрия) и корня кубического (стереометрия).
Вообще говоря, извлечение корня с различными целыми показателями является частным случаем дробной степени. Но к такому пониманию этих алгебраических операции математики подошли только в семнадцатом веке. Неоценимый вклад в достижении обобщенного понимания степенных алгебраических операции внес Рене Декарт.

В свете современных представлений:

Среднее геометрическое значение множества положительных вещественных чисел определяется как результат взаимного умножения этих чисел и извлечения из произведения корня с показателем равным количеству чисел:

Таким образом, мы имеем дело исключительно с положительными вещественными числами и находим такое число, что при замене каждого из этих чисел их произведение не изменяется.
 

Расчет среднего геометрического

Для того чтобы начать онлайн расчет среднего геометрического введите исходные числа в одно из полей ввода-вывода данных.
В первое поле можно ввести последовательность чисел, разделенных точкой с запятой (программа попытается так же преобразовать к стандартному виду, например, вставленную копию последовательности чисел с плавающей точкой, разделенных пробелами, запятой или точкой с запятой).
Во второе поле можно вводить числа по одному - они автоматически будут добавляться к данным первого поля, если расчет не запустился автоматически, кликните по зеленой кнопке, показывающей количество чисел в исследуемом массиве:
 

 

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднего геометрического в истории браузера

Адресную строку с кодом из Ваших данных Вы можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа, цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый, и автоматически начнется расчет среднего геометрического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

Свойства среднего геометрического

1. Среднее геометрическое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.

2. Кроме того среднее геометрическое подчиняется неравенству о средних для множества положительных вещественных чисел

a_min   ≤   a_{ср. гарм}   ≤   a_{ср. геом}   ≤   a_{ср. арифм}   ≤   a _{ср.квадр} ≤   a _max ^[2] ,

то есть для любого множества положительных чисел среднее геометрическое никогда не бывает больше среднего арифметического ^[1]:

 

 

Прикладное значение среднего геометрического

Среднее геометрическое широко используется в демографической статистике, моделирований социального развития общества.
С применением среднего геометрического в экономике расcчитываются финансовые индексы, в физике - коэффициент преломления антибликового напыления, а в вычислительной математике осуществляется сглаживание шумов.

 

P.S. На этой странице используется Бета версия программы расчета среднего геометрического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

 

1. Среднее арифметическое значение (чаще используется термин, просто, "среднее арифметическое" или "среднее") множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

 

2. Среднее степенное значение   s_d  порядка (степени) d от множества заданных чисел a₁+ a₂+ …+ a_n определяется формулой:

 

Среднее арифметическое является степенным средним c d = 1, среднее квадратическое - d = 2, среднее гармоническое можно считать степенным средним порядка d = -1.

 

● Главная ▸ Статьи ▸ Блог ▸ Копилка ✔ Среднее геометрическое - расчет онлайн